Vamos começar com alguns conceitos básicos:
Trigonometria no Triangulo Retângulo
No triangulo retângulo, com vimos em Teorema de Pítagoras, sempre há um angulo reto (90º) que aponta para a hipotenusa, e os catetos.
Aqui na trigonometria chamaremos os catetos de Cateto Oposto e Cateto Adjacente.
As relações básicas na trigonometria são SENO, COSSENO e TANGENTE.
Observe o triângulo retângulo abaixo, onde a é a hipotenusa (lado oposto ao ângulo de 90º), b e c são os catetos do triângulo retângulo(catetos são os lado que formam o ângulo de 90º)

Lembre-se, os catetos variam de nome de acordo com a posição do ângulo
A seguir as relações básicas para trabalharmos no triangulo
Depois de visto as relações vejamos algumas fórmulinhas que devemos guardar em mente.
Na mesma tabela existem:
-COSSECANTE: que nada mais é que o inverso do SENO para descobrir é só inverter as fórmulas
- SECANTE: que é inverso do COSSENO basta inverter as relações
OBS: onde tiver raíz no denominador não esquecer de fazer a RACIONALIZAÇÃO
Conhecendo essa tabela podemos trabalhar e descobrir qualquer lado de um triangulo RETÂNGULO.
Círculo Trigonométrico
Para trabalhar com ângulos maiores ou diferentes que os ângulos da tabela usamos o círculo trigonométrico.
Representando fica assim.

OBS`s: PÍ = 180º, 0,5 = 1/2, o eixo horizontal é o eixo dos cossenos, o eixo vertical é o eixo dos senos, o círculo é separado em 4 quadrantes.
O 1º é o circulo onde encontramos os angulos de 30º, 45º e 60º, e vai aumentando no sentido anti-horário. 2º quadrante, 3º quadrante e 4º quadrante.
Para trabalharmos com o sinal dos senos e cossenos utiliza-se o seguinte raiocínio:
-seno (encontrado no eixo vertical) traça-se a reta até o eixo se bater acima é positivo se bater abaixo neg.
-cosseno (encontrado no eixo horizontal) traç-se a reta até o eixo se bater à direita posit. e esquerda neg.
No círculo observamos que existem ângulos semelhantes e equivalentes que diferenciarão apenas no sinal.
ex: 30º=150º=210º=330º
esses ângulos na hora de utilizar a fórmula os nº serão os mesmos, mudarão o sinal de acordo com o nome (seno e cosseno), e quadrante.
Identidades Trigonométricas
existe uma fórmula muito usadapara calcular angulos que diz:
Sen²x + Cos²x = 1
Chama-se relação fundamental (x nesse caso representa um ângulo qualquer)
Soma e subtração
para somar e subtrair ângulo utilizamos algumas fórmulas vejamos à seguir algumas delas:
SOMA
Sen(A+B) = senA.cosB + senB.cosA
Cos(A+B) = cosA.cosB - senA.senB
Tang(A+B) = tanA + tanB
----------------
1 - tanA.tanB
SUBTRAÇÃO
Sen(A-B) = senA.cosB - senB.cosA
Cos(A-B) = cosA.cosB + senA.senB
Tang(A-B) = tanA - tanB
----------------
1 + tanA.tanB
Arcos Duplos
Quando trabalhamos com o arco referente a um ângulo dizemos que ele é o dobro do seu ângulo.
ex: senX ===> sen2X
Fórmulas dos Arcos
SENO
sen2X = 2.senX.cosX
COSSENO
cos2X = cos²X - sen²x
Para saber cada um usa-se a relação fundamental (sen²x + cos²x = 1) isolando cada um e substituindo na fórmula
ex: sen²x + cos²x = 1 ====> sen²x = 1 - cos²x =====> cos² = 1 - sen²x
substituindo:
cos2X = cos²x - sen²x
cos2X = cos²x - (1-cos²x)
cos2X = 2.cos²x - 1
cos2X = cos²x - sen²x
cos2X = (1-sen²x) - sen²x
cos2X = 1 - 2.sen²x
Espero que tenha conseguido passar algo muito explicativo a vocês!
Um grade abraço!




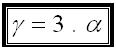


 » x=
» x= 






